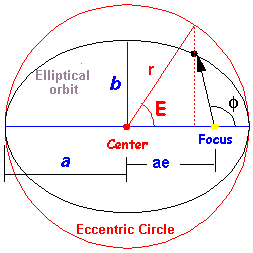
Orbital Angles (Called Anomalies)
- P = period of Orbit
- t = time for position of interest
- T = time of periapsis passage
- e = eccentricity of the orbit
- True (Angle) Anomaly, φ
the angle of the object past periapsis with center the focus
- Mean (Angle) Anomaly, M = 2π(t - T)/P
Actually the time past periapsis put in angle format
- Eccentric (Angle) Anomaly, E
The angle of the object position projected on the reference circle.
Relationships
Find Time given Position
- Determine Eccentric Anomaly
cos E = (e + cos φ)/(1 + e cos φ)
- Kepler's Equation
M = E - e sin E
t = (M/2π)P + T
Example 1:For e = 0.3, φ = 90° find the time past periapsis
cos E = (0.3 - 0)/1 + 0.3) = 0.2308: E = 76.66° = 1.338 rad
M = 1.338 - 0.3 sin(76.7°) = 1.046 rad
t - T = (M/π)P = 0.166 P
For a cirular orbit this would be 0.25 P
Find Position given Time: M = 2π(t-T)/P
- Kepler's Equation
M = E - e sin E
Solve for E given M - use interative procedure.
- cos(φ) = (cos E - e)/(1 - e cos E)
Example 2: For e = 0.3, (t - T)/P = 0.25, find the angle past periapsis
M = 0.25 2π = 1.571
solve 1.571 = E - 0.3 sin E by interative use of the previous solution
E = M + e sin E
- 1st: E = 1.571 + 0.3 sin 90° = 1.871 rad = 107.2°
- 2nd: E = 1.571 + 0.3 sin 107.2° = 1.858 rad = 106.4°
- 3rd: E = 1.571 + 0.3 sin 106.4° = 1.859 rad = 106.5°
- 4th: E = 1.571 + 0.3 sin 106.5° = 1.859 rad
Solution is E = 1.859 rad
cosφ = [cos(106.5°)- 0.3]/[1 - 0.3 cos(106.5°)] = -0.455
φ = 117.1°
For a cicular orbit this would be 90°
Note: All angles are in radians
1 radian = 360/2π = 57.3 degrees
June 10, 2005 - L.Bogan

