Co-orbit Rendezvous - Earth Orbit

Situation:
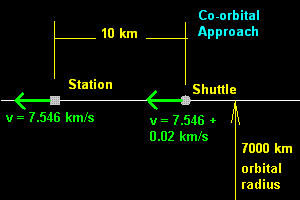
• Shuttle 10 km behind Station in 7000 km radius circular orbit. (v = 7.546 km/s, P = 5828 s = 97.1 min)
• Shuttle attempts to catchup by increasing speed by 0.02 km/s (72 kph)
• In normal circumstance - catchup time = 10 km /0.02 km/s = 500 s = 8.3 min

Orbital Physics
• Increased orbit speed --> Increases Kinetic Energy --> Decreased negative Orbit Energy
• Since E = - k/a the semi-major axis, a, must increase in value (to . This will also increase the period of the orbit (∝ a^3/2) for the Shuttle and it will fall behind the Station.
• At the tme the velocity is increased to 7.566 km/s the Shuttle is at perigee.
The elliptical orbit:
• Semi-major axis, a = 7037.4 km
• Eccentricity, e = 0.0531
• Period, P = 5875 s (97.92 min)
• V_apogee = 7.526 km/s (slower than the Station)
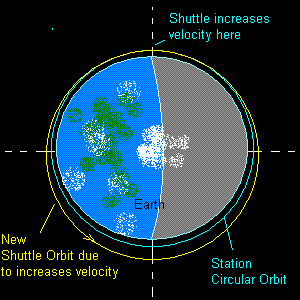
• The Shuttle will rise into a higher orbit and with apogee at 74.8 km higher than the Station.

Rotating Reference Frame Point-of-View

If we were watching from the Space Station, it would appear that when the Shuttle increased its speed, a sideways force acted on it and moved it away from the Earth. This is the fictitious force which creates a Coriolis Acceleration = 2 Δv x ω
where

• ω is the angular velocity of the Station's frame of reference (2π/P = 0.00106945/s )
.
• Δv is the incremental velocity with-respect-to the reference frame (0.02 km/s)
• Acceleration = 0.00004278 km/s²
  Perpendicular motion in 500 s = at²/2 = 5.35 km
• The Shuttle will be over 5 km above the Station when it passes it.
  However, the Shuttle will continue in a circular motion caused by the coriolis acceleration and will drop behind the Station.

Created on ... June 11, 2005