Kepler's Equation Example

Examples in the Use of Kepler's Equation

We will show how to use Kepler's Equation which is

M = E - e sin E

to get the time, t, or position, n, in orbit. An addition relationships

cos n = [cos E - e]/[1 - e cos E]

and

cos E = [cos n + e]/[1 + e cos n]

will be needed.

E = eccentric anomaly measured from perihelion about the center of the elliptical orbit
e = eccentricity of the orbit
M = mean anomaly = 2p t/P
t = time since perihelion passage
P = period of the orbit
n = true anomaly = angle of the object in obit relative to the perihelion

EXAMPLES: An orbit with e = 0.20

Determine the fraction of a period required to travel 1/6 of an orbit past perihelion (60^o).
Determine the angular position past perihelion after 1/6 of the orbital period.

Example 1.
n = 60^o
cos E = (cos 60^o + 0.2)/(1 + e cos 60^o) = 0.46667
E = 1.08528 radians = 62^o.18
M = 1.08528 - 0.20 sin(1.08528 radians) = 0.90839
t/P = M/(2p) = 0.14458

Example 2.
t/P = 1/6 = 0.16667
M = 2p/6 = p/3
Iterative Solution: Kepler's equation must be solved for the eccentric anomaly, E, but the equation is transandental and has no algebraic solution. The solution must be done numerically. As long as the eccentricity is not near 1, an interative solution as follows works well.

E₁ = M + e sin M
E₂ = M + e sin E₁
E₃ = M + e sin E₂
E₄ = M + e sin E₃
....

This is repeated until two succeeding values of E are the same within the precision desired.

Using the values of M and e for this example we get

E₁ = 1.2350
E₂ = 1.2360
E₃ = 1.2361
E₄ = 1.2361 radians

Calculate the true anomaly:
cos(n) = [cos(1.2361) - 0.20]/[1 - 0.20 cos(1.2361)] = 1.3759
n = 1.4328 radians = 82^o.09

Compare these results with a circular orbit, ie e = 0.
In that case the angle would be 60^o and the time would be 0.16667 period.

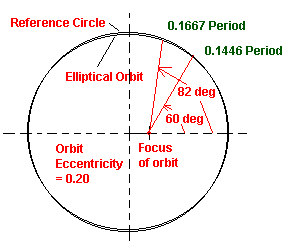The geometry of the example is shown in the diagram to the right. Note how little an eccentricity of 0.2 changes the shape of the ellipse from a circular shape. The biggest difference between the reference circle and the elliptical orbit is the center of reference. The focus of the ellipse is 0.2 of the radius from the center of the ellipse and circle. The angles and times calculated in these examples are shown here. In only 0.1446 of a period the orbiting object will be 60^o from perihelion while if one waits 1/6 of a period it will be 82^o from the perihelion.