The New Orbit of the Spacecraft after Jupiter Encounter

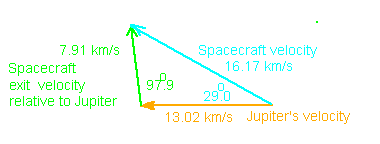The final step in describing the path of the spacecraft is to determine its orbit after leaving the influence of Jupiter. The velocity of the spacecraft relative to Jupiter is the same as when it entered the sphere of influence but now is in a more forward direction by 53^o. When this velocity is transformed to the Sun centered system, the velocity of Jupiter adds to the component of the spacecraft in the forward direction. As you can see in the diagram to the right, the velocity of the spacecraft has increase relative to the Sun to 16.17 km/s from the 9.36 km/s before its encounter with Jupiter . This corresponds to a three-fold increase in kinetic energy of the craft. The energy per mass of the orbit itself has changed from -126.7 to -39.8 (km/s)². The fact that the energy of the orbit is still negative means the orbit is elliptical and the craft is still bound to the Sun. (A zero energy orbit is parabolic while a positive energy orbit is hyperbolic both which allow the craft to escape from the Sun's gravity)

The size, shape and orientation of the new orbit is determined using the same relationship for all elliptical orbits. The steps are as follows:

• Evaluate GM_Sun = 887 AU(km/s)²
• The total energy per mass of the orbit is constant so by evaluating the kinetic and gravitational potential energy at one point in the orbit, we have the value:
  v = 16.17 km/s and r = 5.20 AU
  E = mv²/2 - GM_Sunm/r
  E/m = - 39.8 (km/s)²
• The energy per mass of the spacecraft determines the orbits semi-major axis:
  a = -1/2 *(GM_Sun)/(E/m) =11.16 AU
• This then gives the circular velocity of the orbit:
  v_c = GM_Sun/a = - 2E/m = 8.92 km/s
• The period of the orbit is given by Kepler's third law:
  P = a^3/2 = 37.28 years
• The areal velocity is already know from the velocity and position of the spacecraft
  We need to express velocity in AU/yr rather than km/s: 4.74 km/s = 1 AU/yr
  A = r v_/2 where v_ = 16.17km/s cos 29^o
  v_ = 14.15 km/s = 2.985 AU/yr
  A = 7.765 (AU)²/yr
• The other method of determining areal velocity gives us the eccentricity of the orbit.
  A = area of ellipse/period = pa²(1 - e²)^1/2/P
  1 - e² = 0.5474 and e = 0.673
• We now know the size and shape of the orbit and can determine the extent of the orbit. r_p = a (1 - e) = 3.64 AU
  r_a = a (1 + e) = 18.67 AU
  The orbit reaches past that of Saturn but not quite to that of Uranus
  The orbit does not cross that of Mars but does enter the asteroid belt.
• The final parameter is the true anomaly as determined by the angle the craft is from perihelion of the new orbit.
  Solve r = a (1 - e²)/(1 + e cos q) for q
  cos q = [a (1 - e²)/r - 1]/e
  q = 75.^o1
• The graphics shows the new orbit relative to the old one.

Since the spacecraft will cross the orbit of Saturn, if the timing were right, the craft could get a boost from Saturn to increase its energy even more and make it to Uranus, Neptune or possibly escape the Sun's gravity all together.

Back to Main Page